Distances
Dans sa conférence intitulée Histoire d'une plante banale : les rosiers entre histoire des sciences et histoire culturelle, Cristiana Oghina-Pavie nous présente ce schéma :

(Cliquer pour agrandir)
Source : Mathilde Liorzou et al., Nineteenth century French rose (Rosa sp.) germplasm shows a shift over time from a European to an Asian genetic background, Journal of Experimental Botany, Volume 67, Issue 15, August 2016, Pages 4711–4725
Licence Creative Commons BY
Chaque point de couleur représente une variété de rosier, et les distances entre les points sont censées correspondre à un indice d'éloignement génétique entre les individus (le calcul ayant servi à construire cet indice est détaillé dans l'article de Liorzou et al. 2016). Plus il y aura de différences entre les génomes de deux variétés de rosiers, plus les points correspondant à ces rosiers seront éloignés sur le dessin.
Cette représentation graphique m'a beaucoup étonné. Ma confusion pourrait se résumer à la question suivante : que faire si quatre variétés ont toutes "la même taille de différence" entre elles ? Comment dessiner quatre points équidistants les uns des autres, dans un plan ?
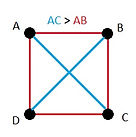
Je m'étais déjà posé la question lors de l'écriture de cet article, et j'avais (trop ?) rapidement abandonné l'idée de munir d'outils graphiques la méthode que j'y proposais - précisément à cause de ce genre d'impossibilités géométriques. Dans le présent article nous allons donc nous pencher sur la notion de distance, que nous avions survolée précédemment.
UNE FAÇON DE FORMALISER LA DISTANCE
Qu'est-ce que c'est, une distance ? Dans une de ses acceptions, le mot désigne un nombre, qui quantifie un aspect de la relation de deux objets l'un par rapport à l'autre. Notons tout d'abord que Liorzou et al. utilisent une distance dite "euclidienne", et nous allons de ce pas expliciter de quoi il s'agit. Imaginons trois points A, B, C et trois critères liés à une manière de décrire - avec des nombres - leur disposition relative dans l'espace.
1) Le critère de séparation considère que l'affirmation "La distance entre A et B est nulle" et l'affirmation "Les points A et B sont identiques" sont équivalentes.
2) Le critère de symétrie considère que la distance entre A et B est nécessairement strictement égale à la distance entre B et A.
3) Le critère d'inégalité triangulaire considère que la distance entre A et B est nécessairement égale ou inférieure à la somme des distances AC et CB.
N'importe quel calcul portant sur A, B et C qui respecte ces trois critères sera considéré comme le calcul d'une "distance euclidienne". Cela peut paraître une manière inutilement compliquée de raconter un concept somme toute assez intuitif. Mais le fait de le formaliser ainsi va nous aider à savoir si ce concept peut s'appliquer entre des objets de sciences humaines. Si cette notion spécifique de distance peut par exemple être utilisée de manière pertinente pour raconter des relations entre des concepts, ou des relations amicales entre des individus.
DES CAS QUI FONCTIONNENT PLUS OU MOINS BIEN
-
La distance spatiale
Pour commencer, ce qu'on appelle généralement la distance spatiale est une distance euclidienne entre deux positions : si deux objets occupent strictement la même position dans l'espace, alors leur distance est nulle, et réciproquement (séparation), la distance entre deux points est la même à l'aller et au retour (symétrie), et la ligne droite est le plus court chemin entre deux points (inégalité triangulaire).
-
La distance conceptuelle
Considérons ensuite l'exemple de la "distance conceptuelle" entre les cartes d'un jeu de cartes. Nous l'avions définie comme ceci : On s’adresse à un groupe et on demande à chaque membre de « réunir en tas les cartes qui vont ensemble ». Suite à quoi, on pourrait définir une sorte de « distance » entre deux cartes données : plus des cartes auront été mises fréquemment dans un même tas, plus on les considérera comme « proches » [aux yeux du groupe].
Il est facile de démontrer qu'un tel indicateur respecte le critère de symétrie. Pour ce qui est du critère d'inégalité triangulaire, les choses se compliquent.
Dans ce cadre définitionnel, on peut tout à fait imaginer un scénario où on a demandé à 100 personnes de procéder à une catégorisation avec un paquet de trois cartes, A, B et C, et la moitié des enquêté.e.s a placé A et B (mais pas C) dans un même tas, et les 50 autres ont placé B et C (mais pas A) dans un même tas.

Autrement dit, les membres du groupe dont nous essayons de saisir les modes de classification ont considéré que A et B étaient proches ou que B et C étaient proches, mais tous sont d'accord pour dire que A et C ne le sont pas. Cela constitue en apparence une transgression du critère d'inégalité triangulaire : La distance AC pourrait bien ici être plus grande que la somme des distances AB + BC.
Toutefois, la population de nos enquêté.e.s a visiblement utilisé au moins deux logiques très différentes, deux approches catégorisantes, pour procéder à la mise en tas de A B et C. C'est le fait de les agglomérer entre elles au sein d'un même indicateur qui conduit à cette situation paradoxale où AC > AB + BC.
Remarquons cependant que si on applique le même outil à chaque approche catégorisante prise individuellement, le critère d'inégalité triangulaire est à nouveau respecté. On en revient donc à une conclusion esquissée précédemment : une heuristique "Splitter" est la bienvenue ici.
Mais une seconde difficulté émerge quand on aborde le critère de dissociation. Par définition, une carte donnée sera toujours placée dans le même tas qu'elle-même. Ce qui implique que, quel que soit le calcul utilisé pour construire le nombre 'distance conceptuelle' à partir du nombre 'fréquence à laquelle les objets sont placés dans un même tas', il faut que ce calcul donne zéro quand la fréquence est de 100% - sans quoi, notre indicateur verra une distance conceptuelle non-nulle entre une carte et elle-même.
Or, si nous dimensionnons notre calcul de la sorte, cela implique que dans le cas hypothétique où un groupe a systématiquement placé le 4 de pique et le 4 de cœur dans un même tas, alors aux yeux de notre indicateur le 4 de pique et le 4 de cœur sont 'le même objet conceptuel' pour ce groupe - ce qui est probablement faux !
-
La distance amicale
Tournons-nous maintenant vers le concept de distance amicale, au sens de "À quel point deux individus sont proches". Cette heuristique correspond-elle à une distance euclidienne ? Ici, les problèmes abondent. Pour commencer, l'idée qu'une proximité amicale infinie entre deux individus correspondrait nécessairement à une ressemblance telle entre ces individus qu'il convient de les considérer comme occupant une même position dans l'espace des relations sociales fait déjà hausser les sourcils.
Mais le principal problème n'est pas là. Dans une définition naïve de ce qu'est l'amitié, rien ne semble garantir la réciprocité symétrique. En d'autres termes, Alice peut se considérer comme extrêmement proche de Bob, tandis que Bob la voit comme une simple connaissance. Il est théoriquement possible d'objectiver le concept d'amitié autrement qu'en recueillant les ressentis subjectifs des intéressé.e.s, via des approches qui conservent la symétrie - mais il semble que cela nous fait sortir de l'acception la plus intuitive de ce que c'est que l'amitié.
Enfin, il y a aussi un problème avec le critère d'inégalité triangulaire. La situation où Alice et Cynthia se détestent mais sont toutes les deux très proches de Bob constitue a priori une entorse à l'inégalité triangulaire : AC > AB + BC. C'est pourquoi, à moins d'utiliser une définition atypique du concept d'amitié, la distance amicale serait plutôt à considérer comme une distance non-euclidienne.
Je suis très ignorant de tout ce qui touche à la géométrie des espaces munis de distances non-euclidiennes. Je me garderai donc bien de recommander tel ou tel outil ici, et je me contenterai de remarquer que les propriétés de tels espaces ont été et sont encore étudiés.
CONCLUSION
Revenons finalement à nos rosiers, et à ce nuage de points dessiné sur la base d'un indice de distance génétique. Comment une telle chose est-elle possible ? Eh bien… il semble qu'elle ne l'est pas réellement. L'astuce consiste à admettre qu'on va fatalement faire un erreur lors du passage à la 2D : certaines distances seront déformées, étirées, comprimées. Mais cette erreur est calculable, en regardant la différence entre la distance génétique d'origine et la distance entre les points du dessin. La somme de toutes les erreurs est appelée le "stress" du dessin. Et puisque ce dernier est calculable, on peut rechercher la représentation graphique où le "stress" est minimum.
Remarquons que le problème du stress minimal possède une résolution connue quand toutes les distances mises en jeu sont euclidiennes. Cette résolution est homogène à une analyse en composantes principales. Un petit script en bas de cette page permet de transformer un tableau de distances euclidiennes dans un espace à n dimensions en un tableau des coordonnées des points correspondants, projetés dans un plan. Ce script évalue aussi le "stress" généré lors de la projection.
Des outils existent aussi pour approcher le stress minimal dans le cas de distances non-euclidiennes, mais ce sont des procédés mathématiques que je ne comprends pas suffisamment bien pour en faire un outil intégré à ce site.
D'une manière similaire à ce qui se produit quand on projette un nuage de points depuis un espace vers un plan, le passage du concept de 'distance' d'un champ de recherche à un autre se fait potentiellement de manière imparfaite. Les choses sont déformées, certaines propriétés du "territoire" ne sont pas respectées sur la "carte". Il se produit une sorte de "stress" conceptuel.
Mais peut-être est-il plus intéressant de manier des objets conceptuels imparfaits mais dont l'imperfection est connue, que de se limiter à des concepts qui reflètent parfaitement ce qu'ils servent à raconter - car il reste à prouver qu'une telle perfection existe, que ce soit parmi les concepts quantitatifs ou qualitatifs.
.
.
Posté le 26/02/2022